BSM Application 4
The reader not acquainted with the BSM theory should read first the article "Breaf Introduction to BSM theory" in order to understand the presented method of modeling.
The physical models of the atoms provide a great opportunity for a modeling of different structures in nanotechnology. Such modeling could serve as a preliminary design of molecular structures in which the building blocks are the selected atoms. In such design, not only the possible combinations could be examined, but the position and orientation of any quantum orbit can be identified.
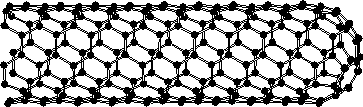
Fig. 1. provides an axonometric view of a part of single-walled carbon nanotube, as known by the current knowledge. The cylindrical part of this nanotube does not contain any defect and all ring structures involves 6 carbon. If imaging that the cylindrical surface of such nanotube is unfolded it will be a flat sheet without bumps or dimples. If some ring structure, however, contains 5 carbon atom, a bump or dimple will occur. The closed end of the nanotube should contain such structures.

Fig. 1
Fig. 2 shows a sheet of the unfolded cylindrical wall with identified valence of the chemical bonds, so that the four valences of all carbon atoms (excluding the edge atoms) are connected.
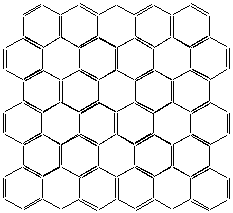
Fig. 2
Let considering the hexagonal ring as a unit structure of the sheet. Then the sheet is comprised of two types of ring structures:
- ring structure of I-st type (containing only single valence bonds)
- ring structures of II-nd type (containing tree single valence bonds and three second valence bonds).
Fig. 3 shows the overall shapes of the neutron, proton, deuteron and He with the possible positions of the quantum orbits. The surface in which the quantum orbit lies in fact intercept the average plane of the proton at right angle. The two separated orbits of the He (not shown) have four leafs and also are perpendicular to the average proton planes.
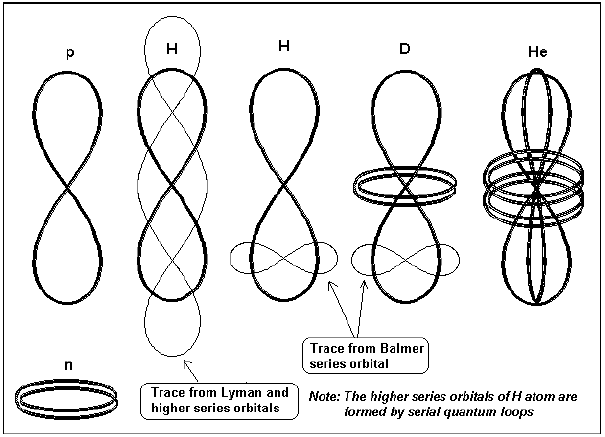
Fig. 3
Fig. 4 shows the physical model of the Carbon atom in which the protons and neutrons are presented by symbolic notations. The left part of the figure shows an axonometric view of the carbon atom. The He nucleus in the carbon nucleus with its long axis define the polar axis of carbon nucleus (valid also for all atoms). The two protons (deuterons) in the top pole have a limited angular freedom in the plane of the drawing. The two protons (deuterons) in the bottom pole have a limited angular freedom in a plane perpendicular to the drawing. The right part of the figure shows the possible dimensions of the quantum orbits, denoted by the subharmonic number of the oscillating electron and corresponding to electron energies as shown in the Table at the left side of the figure (see Chapter 3 of BSM). The quantum orbits as a rule of drawing in BSM models are drawn by a dashed line. The proton dimensions and the size of the possible quantum orbits are in one and a same scale.
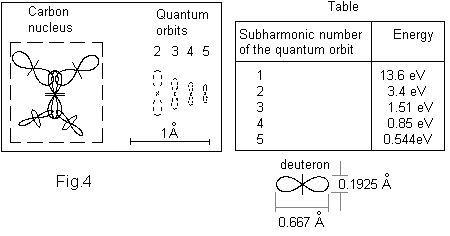
Fig. 5 provide an axonometric view of a sheet, corresponding to unfolded cylindrical part of single walled carbon nanotube. The rings of I-st type are clearly distinguishable from the rings of II-nd type. The protons, involved in the second valence bonds lie in plane perpendicular to the sheet plane. In the same figure all quantum orbits providing chemical bonding are also shown. The quantum orbits of the free (nod bound) protons in the edges a shown as well.
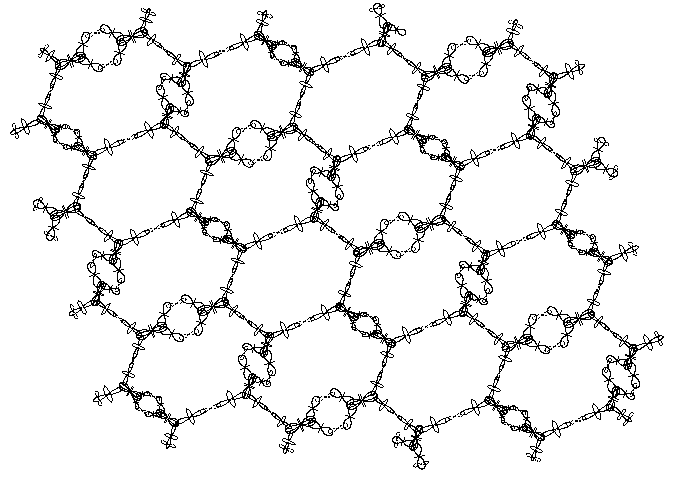
Fig. 5
From Fig. 2 and Fig. 5 it is evident that every ring structures of I-st type has 3 neighbors of same type and 3 neighbors of second type, while every ring structures of II-nd type has 6 neighbors of same type. Therefore the overall ratio between the two types ring structures is 1/2.
Fig. 6 shows a zoomed section from the carbon wall sheet, so the orbital position are shown more clear. The two orbitals of He nucleus of carbon atoms are not shown. If regarding the sheet as built of lower level atomic structures it contains only He nuclei and deuterons. However, the four deuterons are very strongly bound to the He nuclei assuring the compactness of the carbon atom. These type of nuclear bonds between protons and neutrons are hold by very strong forces, whose origin is analyzed in details in BSM theory. In comparison to them the electronic bonds forming quantum orbits are extremely weak.
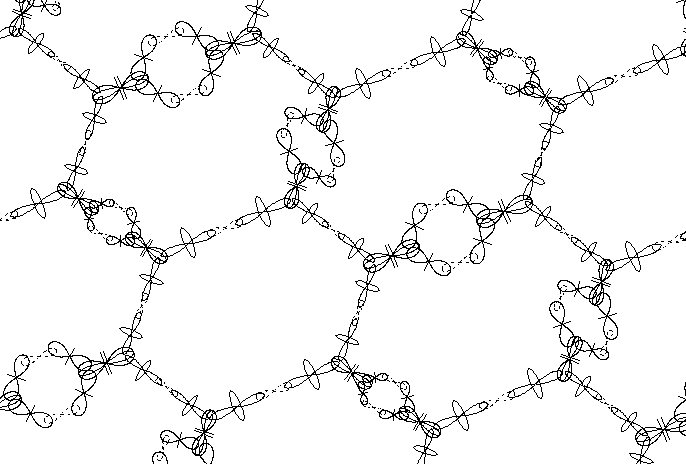
Fig. 6
It is evident that the ring of I-st type could be a pentagon instead of hexagon and will have 5 neighboring rings of second order. Then the single wall will get bending.
Not only the structural design but the the conductive properties of the designed structures also could be forecast, if preliminary knowledge about the orbital distances and positions corresponding to bandgap between a conductive and isolating states are available (also a knowledge about the spatial configuration of the proximity electrical field of the proton and its possible influence from the closely spaced protons, but this could be obtained by approximate theoretical modeling). This is apparent from the concept of the BSM theory about the electrical field of the elementary particles, as a result of Intrinsic energy balance of the system: particle - vacuum space (structured space) in which strong forces are also involved.
Examining the quantum orbits involved in the chemical bonds it is evident that the plane orientation of the quantum orbits in the single valence bonds are different from the plane orientations of the second valence bonds. For electrical neutral state of the sheet all quantum orbits contain two electrons with oposite quantum mechanical spins (referenced to the proton twisting). It is possible, however, in conditions of very strong external electrical field, the local fields of the protons to be biased. Then one of the two electrons in the chemical bond quantum orbits might be separated as a free electron providing a conductivity. A quantum orbit with only one electron is also possible, but its shape and also a subharmonic number could be possibly changed.
The suggested method could be used successfully also for thin crystal layers grown by molecular beam epitaxy. Fig. 6, for example shows the atom of gold in two views: the right side view is a polar view, while the left side view is a polar sectional view in which only the protons (deuterons) closer to the sectional plane are shown. He nuclei, as most dens atomic structures are always in the middle of the atomic nucleus and aligned with the polar axis of the atom.
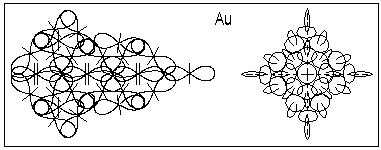
Fig. 7
In the next page a comparison between image of two planes of gold crystal and the model design using the physical structures of the atom of gold are shown. Click here